UNIDAD 2

TRANSFORMACIONES GEOMETRICAS

Las transformaciones geométricas son la o las operaciones geométricas que permiten crear una nueva figura a partir de una previamente dada. la nueva figura se llamará "homólogo" de la original.

las transformaciones se clasifican en:

• Directa: el homólogo conserva el sentido del original en el plano cartesiano.
• Inversa: el sentido del homólogo y del original son contrarios. 

2.1 Transformaciones bidimencionales

2.1.1 Traslación. 

Se aplica una traslación en un objeto para cambiar su posición a lo largo de la trayectoria de una línea recta de una dirección de coordenadas a otra. Convertimos un punto bidimensional al agregar las distancias de traslación, tx y ty la posición de coordenadas original (x,y).

2.1.2 Rotación.

Se aplica una rotación bidimensional en un objeto al cambiar su posición a lo largo de la trayectoria de una circunferencia en el plano de xy . Para generar una rotación, especificamos un ángulo de rotación θ y la posición (x r , y r ) del punto de rotación (o punto pivote) en torno al cual se gira el objeto.

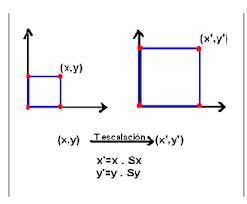
2.1.3 Escalación.

Una transformación de escalación altera el tamaño de un objeto. Se puede realizar esta operación para polígonos al multiplicar los valores de coordenadas (x, y) de cada vértice por los factores de escalación s x y s  y para producir las coordenadas transformadas (x’, y’ ).

2.2 Coordenadas homogéneas y representación matricial. 

En las aplicaciones de diseño y de creación de imágenes, realizamos traslaciones, rotaciones y escalaciones para ajustar los componentes de la imagen en sus posiciones apropiadas. En este tema consideramos cómo se pueden volver a formular las representaciones de la matriz de modo que se pueden procesar de manera eficiente esas secuencias de transformación. Es posible expresar cada una de las transformaciones básicas en la forma de matriz general con las posiciones de coordenadas P y P’ representadas como columnas de vector.2.15.P'=M1·P+M.

La matriz M1 es una matriz de 2 por 2 que contiene factores de multiplicación y M2 es una matriz de columnas de dos elementos que contiene términos de traslación. Para la traslación, M1 es la matriz de identidad. Para la rotación o la escalación M2 contiene los términos de traslación asociados con el punto pivote o el punto fijo de escalación.

2.3 Composición de transformaciones bidimensionales. 

Con las representaciones de matriz del tema anterior, podemos establecer una matriz para cualquier secuencia de transformaciones como una matriz de transformación compuesta al calcular el producto de la matriz de las transformaciones individuales. La creación de productos de matrices de transformación a menudo se conoce como concatenación o composición de matrices.

Traslaciones, rotaciones y escalaciones Traslaciones Se se aplican dos vectores de traslación sucesivos (tx1, t y1) y (tx2 , t  y2 ) en la posición de coordenadas P, la localización transformada final P, la localización transformada final P’ se calcula como:2.23.P'=T(t x2,t2)·T(tx1,ty1)·P}{=T(tx2, 2)·T(t x1,t y1)}{·P.

2.3.1 Traslaciones, rotaciones y escalaciones.  

Con las representaciones de matri, podemos establecer una matriz para cualquier secuencia de transformaciones como una matriz de imformacion compuesta al calcular el producto de la matriz de las transformaciones individuales. la creacion de productos de matrices de informacion a menudo se conoce como concatenacion o composicion de matrices. 

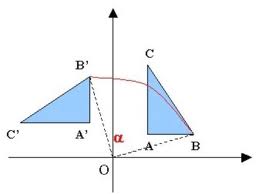
 2.3.2 Rotación de punto de pivote general. 

Con un paquete gráfico que sólo ofrezca una función de rotación para girar objetos con respecto del origen de las coordenadas, podemos generar casi cualquier punto pivote seleccionado (xr , yr) al realizar la siguiente secuencia de operaciones de traslación-rotación-traslación.

1. Traslade el objetivo de modo que se mueva la disposición del punto pivote al origen de las coordenadas.
2. Gire el objeto con respecto del origen de las coordenadas.
3. Traslade el objeto de manera que se regrese el punto pivote a su posición a su posición original.

2.3.3 Escalación del punto fijo general.  

La siguiente figura ilustra una secuencia de transformación para producir escalación con respecto de una posición fija seleccionada (xf, yf) al utilizar una función de escalación que sólo puede escalar en relación con el origen de las coordenadas.

1. 1Traslade el objeto de modo que el punto fijo coincida con el origen de las coordenadas.
2. 2 Escale el objeto con respecto del origen de las coordenadas.
3. 3 Utilice la traslación inversa del paso 1 para regresar el obejto a su posición original.

 2.3.4 Propiedades de concatenación. 

La multiplicación de matrices es asociativa. Para tres matrices cualesquiera A, B y C, elproducto matricial A·B·C se puede lelvar a cabo al multiplicar primero a por B o multiplicarprimero B por C:

A· B·C=( A· B)·C=A·( B·C)

Por tanto, podemos evaluar los productos matriciales al utilizar una agrupación asociativa ya sea de izquierda a derecha o de derecha a izquierda. Por otro lado, los productos de la transformación tal vez no sean conmutativos. En general el producto matricial A·B no es igual que B·A. Esto significa queremos trasladar y girar un objeto, debemos tener cuidado sobre el sentido en que se evalúa la matriz compuesta.

2.4 Transformación ventana-área de vista.  

Algunos paquetes gráficos permiten que el programador especifique coordenadas de primitivas de salida en un sistema de coordenadas de mundo de punto flotante, usando las unidades que sean relevantes para el programa de aplicación: angstroms, micras, metros, millas, años luz, etcétera.

Esta correspondencia se puede efectuar si el programador de la aplicación proporciona al paquete gráfico una matriz de transformación para la correspondencia. Otra forma es que el programador de la aplicación especifique una región rectangular en coordenadas de mundo, llamada ventana de coordenadas mundiales y una región rectangular correspondiente en coordenadas de pantalla, llamada área de vista, con la cual se establece la correspondencia de la ventana de coordenadas mundiales. La transformación que establece la correspondencia entre la ventana y el área de vista se aplica a todas las primitivas de salida en coordenadas de mundo para que correspondan a coordenadas de pantalla.

COLOCACIÓN DE VENTANAS Y RECORTE

Los programas de aplicaciones definen imágenes en un sistema de coordenadas mundiales. Este puede ser cualquier sistema de coordenadas Cartesianas que un usuario halle conveniente.  Comúnmente, un paquete de graficas permite a un usuario especificar qué área de la definición de la imagen se desplegara y donde se colocara en el dispositivo de despliegue. Podría elegirse una sola área para el dispositivo de despliegue o bien podrían seleccionarse varias áreas. Estas áreas pueden colocarse en localidades aparte del despliegue o bien un área puede servir como una pequeña inserción en un área mayor. Este proceso de transformación implica operaciones para trasladar y escalar áreas seleccionadas y para borrar partes de la imagen que estén fuera de las áreas. Estas operaciones se conocen como colocación de ventanas y recorte.

CONCEPTOS DE COLOCACIÓN DE VENTANAS

Un área rectangular que se especifica en coordenadas mundiales se denomina ventana. El área rectangular en el dispositivo de despliegue en el cual se coloca la ventana se llama puerta de visión. Esta planimetría se llama transformación de la visión o bien transformación de normalización.

 2.5 Transformaciones de la composición general y de eficiencia computacional

Una transformación bidimensional general, que representa una combinación de traslaciones, rotaciones y escalaciones. Solo necesitamos efectuar cuatro multiplicaciones y cuatro adiciones para transformar las posiciones de las coordenadas. Este es el número máximo de cálculos que se requieren para cualquier secuencia de transformación, una vez que se han concatenado las matrices individuales y evaluadas los elementos de la matriz compuesta. Sin concatenación, se aplicarían las transformaciones individuales una a la vez y se podría reducir en forma considerable el número de cálculos.

2.6 Representación matricial de transformaciones tridimensionales.  

Sí como las transformaciones bidimensionales se pueden representar con matrices de3 X 3 usando coordenadas homogéneas, las transformaciones tridimensionales se pueden representar con matrices de 4 X 4, siempre y cuando usemos representaciones de coordenadas homogéneas de los puntos en el espacio tridimensional. Así, en lugar de representar un punto como (x, y, z ), lo hacemos como (x, y, z, W ), donde dos de estos cuádruplos representan el mismo punto si uno es un multiplicador distinto de cero del otro: no se permite el cuádruplo (0, 0, 0, 0). Como sucede en el espacio bidimensional.

2.7 Composición de transformaciones  tridimensionales.

La transformación de un punto a esta forma se denomina homogeneización, igual que antes. Además los puntos cuya coordenada W es cero se llaman puntos en el infinito. También existe una interpretación geométrica. Cada punto en el espacio tridimensional se representa con una línea que pasa por el origen en el espacio de cuatro dimensiones, y las representaciones homogeneizadas de estos puntos forman un subespacio tridimensional de un espacio de cuatro dimensiones definido por la ecuación

W = 1.